MAGNABEND - 기본 설계 고려 사항
기본 자석 디자인
Magnabend 기계는 듀티 사이클이 제한된 강력한 DC 자석으로 설계되었습니다.
기계는 3가지 기본 부품으로 구성됩니다.
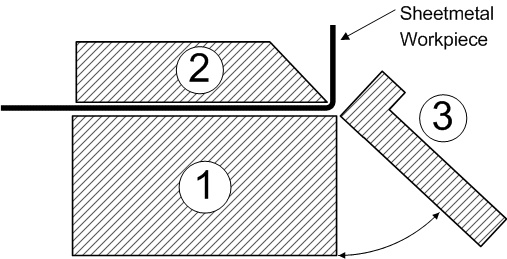
기계의 바닥을 형성하고 전자석 코일을 포함하는 자석 본체.
자석 베이스의 극 사이에 자속의 경로를 제공하여 판금 공작물을 고정하는 클램프 바입니다.
자석 본체의 전면 가장자리로 회전하고 작업물에 굽힘력을 가하는 수단을 제공하는 굽힘 빔.
자석 본체 구성
마그넷 본체는 다양한 구성이 가능합니다.
다음은 Magnabend 기계에 사용된 2가지입니다.
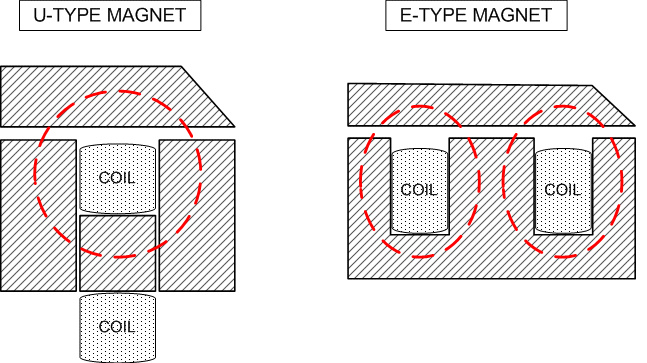
위의 그림에서 빨간색 점선은 자속 경로를 나타냅니다."U-Type" 디자인에는 단일 플럭스 경로(극 쌍 1개)가 있는 반면 "E-Type" 디자인에는 플럭스 경로 2개(극 쌍 2개)가 있습니다.
자석 구성 비교:
E형 구성은 U형 구성보다 더 효율적입니다.
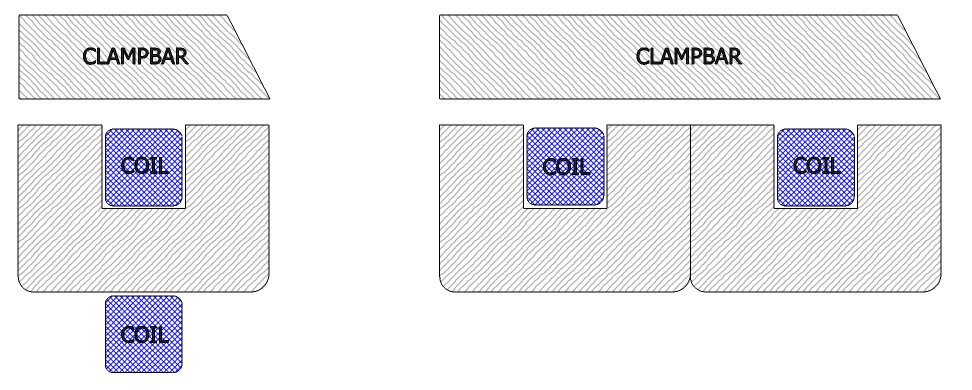
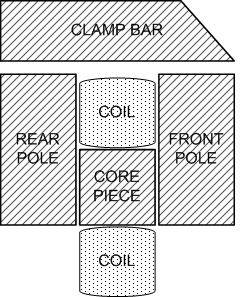
이것이 왜 그런지 이해하려면 아래 두 그림을 고려하십시오.
왼쪽은 U형 자석의 단면이고, 오른쪽은 동일한 U형 자석 2개를 조합하여 만든 E형 자석입니다.각 자석 구성이 동일한 암페어 회전수를 가진 코일에 의해 구동되는 경우 분명히 이중화 자석(E형)은 두 배의 클램핑력을 갖게 됩니다.그것은 또한 두 배의 강철을 사용하지만 코일에 더 이상 와이어를 사용하지 않습니다!(긴 코일 설계를 가정).
("E" 디자인에서 코일의 2개의 다리가 더 멀리 떨어져 있기 때문에 소량의 추가 와이어가 필요하지만, 이 추가 와이어는 Magnabend에 사용되는 것과 같은 긴 코일 디자인에서 중요하지 않습니다.
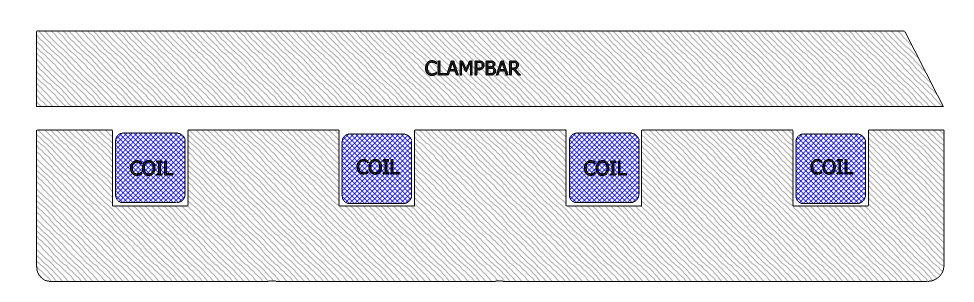
슈퍼 마그나벤드:
더 강력한 자석을 만들기 위해 "E" 개념을 다음과 같이 확장할 수 있습니다. 이러한 이중 E 구성:
3D 모델:
아래는 U형 자석의 기본 부품 배열을 보여주는 3D 도면입니다.
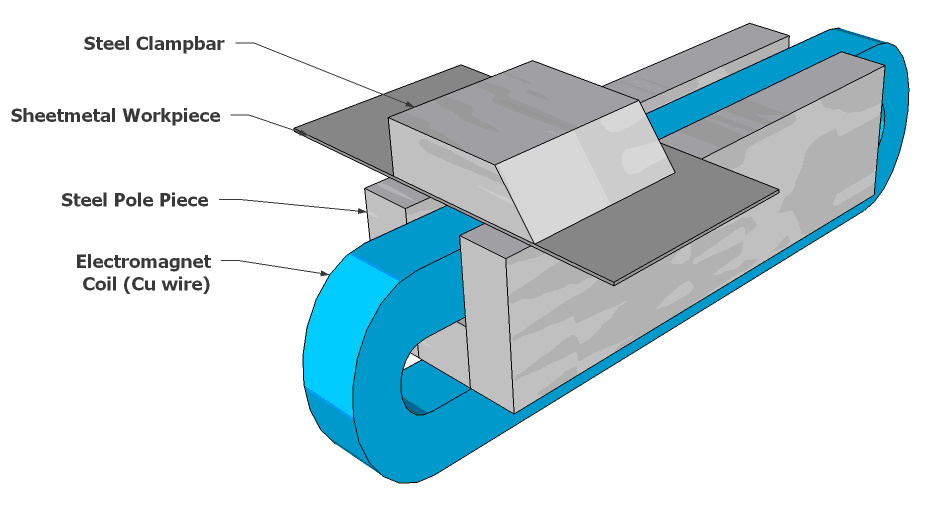
이 디자인에서 전면 및 후면 기둥은 별도의 부품이며 볼트로 코어 부품에 부착됩니다.
원칙적으로 단일 강철 조각으로 U형 자석 본체를 가공하는 것이 가능하지만 코일을 설치할 수 없으므로 코일을 제자리에서(가공된 자석 본체에) 감아야 합니다. ).
생산 상황에서 코일을 개별적으로 감을 수 있는 것이 매우 바람직합니다(특수 포머에).따라서 U자형 디자인은 제조된 구조를 효과적으로 지시합니다.
반면에 E형 디자인은 자석 본체를 가공한 후 미리 만들어진 코일을 쉽게 설치할 수 있기 때문에 단일 강철 조각으로 가공된 자석 본체에 적합합니다.단일 조각 자석 본체는 또한 자속(따라서 클램핑 힘)을 약간 감소시키는 구성 간격이 없기 때문에 자기적으로 더 잘 작동합니다.
(1990년 이후에 만들어진 대부분의 Magnabends는 E-type 디자인을 채택했습니다).
마그넷 구성 재료 선택
자석 본체와 클램프 바는 강자성(자화 가능한) 재료로 만들어야 합니다.강철은 단연코 가장 저렴한 강자성 재료이며 확실한 선택입니다.그러나 고려할 수 있는 다양한 특수강이 있습니다.
1) 규소강 : 고저항강으로 일반적으로 박판으로 사용되며 AC변압기, AC자석, 계전기 등에 사용된다. DC자석인 Magnabend에는 그 특성이 요구되지 않는다.
2) 연철 : 이 재료는 잔류 자기가 낮아 Magnabend 기계에 적합하지만 물리적으로 부드러워 쉽게 찌그러지거나 손상될 수 있습니다.잔류 자기 문제를 다른 방법으로 해결하는 것이 좋습니다.
3) 주철 : 압연강만큼 쉽게 자화되지 않으나 고려할 수 있다.
4) 스테인리스강 유형 416: 강철만큼 강하게 자화할 수 없고 훨씬 더 비쌉니다(그러나 자석 본체의 얇은 보호 캡핑 표면에 유용할 수 있음).
5) 스테인리스강 Type 316 : 강철의 비자성 합금이므로 전혀 적합하지 않습니다(위의 4번 제외).
6) 중간 탄소강, K1045 유형 : 이 재료는 자석(및 기계의 기타 부품) 구성에 매우 적합합니다.공급된 상태에서 상당히 단단하고 기계 가공도 잘 됩니다.
7) 중간 탄소강 유형 CS1020 : 이 강은 K1045만큼 단단하지는 않지만 더 쉽게 구할 수 있으므로 Magnabend 기계 구성에 가장 실용적인 선택이 될 수 있습니다.
필요한 중요한 속성은 다음과 같습니다.
높은 포화 자화.(대부분의 강철 합금은 약 2 Tesla에서 포화됨),
유용한 섹션 크기의 가용성,
우발적 손상에 대한 내성,
가공성 및
합리적인 비용.
중간 탄소강은 이러한 모든 요구 사항에 잘 맞습니다.저탄소강도 사용할 수 있지만 우발적 손상에 덜 저항합니다.Supermendur와 같은 다른 특수 합금도 존재합니다. 이 합금은 포화 자화가 더 높지만 강철에 비해 가격이 매우 높기 때문에 고려하지 않아야 합니다.
그러나 중간 탄소강은 골칫거리가 되기에 충분한 약간의 잔류 자기를 나타냅니다.(잔류 자기 섹션 참조).
코일
코일은 전자석을 통해 자화 플럭스를 구동하는 것입니다.자화력은 권선 수(N)와 코일 전류(I)의 곱일 뿐입니다.따라서:

N = 회전 수
I = 권선의 전류.
위의 공식에서 "N"이 나타나는 것은 일반적인 오해로 이어집니다.
회전 수를 늘리면 자화력이 증가한다고 널리 가정되지만 일반적으로 추가 회전은 전류 I를 감소시키기 때문에 일반적으로 발생하지 않습니다.
고정 DC 전압이 공급되는 코일을 고려하십시오.권선 수가 2배가 되면 권선의 저항도 2배가 되어(긴 코일에서) 전류가 반으로 줄어듭니다.순 효과는 NI가 증가하지 않습니다.
NI를 실제로 결정하는 것은 턴당 저항입니다.따라서 NI를 늘리려면 와이어의 두께를 늘려야 합니다.추가 회전의 가치는 전류를 감소시켜 코일의 전력 손실을 감소시킨다는 것입니다.
설계자는 와이어 게이지가 코일의 자화력을 실제로 결정한다는 점을 염두에 두어야 합니다.이것은 코일 설계의 가장 중요한 매개변수입니다.
NI 제품은 종종 코일의 "암페어 턴"이라고 합니다.
얼마나 많은 암페어 회전이 필요합니까?
강철은 약 2 Tesla의 포화 자화를 나타내며 얻을 수 있는 클램핑 력에 대한 근본적인 한계를 설정합니다.
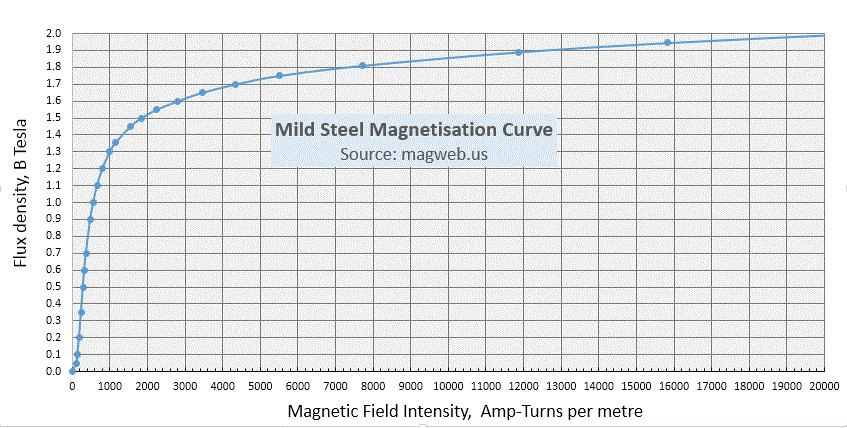
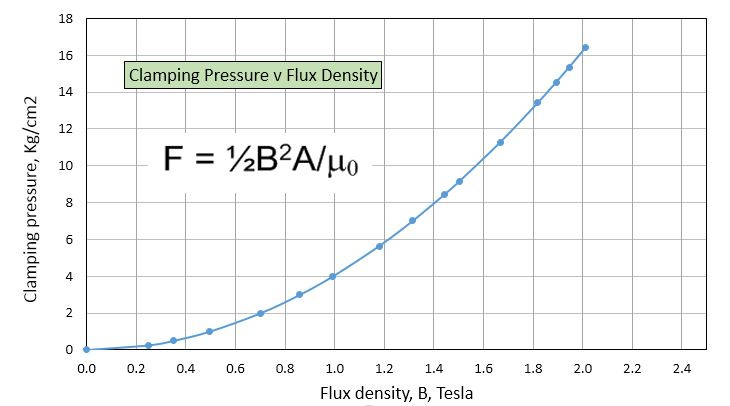
위의 그래프에서 우리는 2 Tesla의 자속 밀도를 얻는 데 필요한 전계 강도가 미터당 약 20,000 암페어 턴임을 알 수 있습니다.
이제 일반적인 Magnabend 설계의 경우 강철의 자속 경로 길이는 약 1/5미터이므로 포화를 생성하려면 (20,000/5) AT, 즉 약 4,000AT가 필요합니다.
비자성 갭(즉, 비철 가공물)이 자기 회로에 도입된 경우에도 포화 자화가 유지될 수 있도록 이보다 더 많은 암페어 회전을 갖는 것이 좋을 것입니다.그러나 추가 암페어 회전은 전력 손실이나 구리선 비용, 또는 둘 모두에서 상당한 비용이 들 때만 얻을 수 있습니다.따라서 타협이 필요합니다.
일반적인 Magnabend 설계에는 3,800암페어 회전을 생성하는 코일이 있습니다.
이 수치는 기계의 길이에 의존하지 않습니다.동일한 자기 설계가 기계 길이 범위에 적용되면 기계가 길수록 더 두꺼운 와이어가 덜 감길 것입니다.더 많은 총 전류를 소비하지만 동일한 암페어 x 회전 곱을 가지며 단위 길이당 동일한 클램핑력(및 동일한 전력 손실)을 갖습니다.
듀티 사이클
듀티 사이클의 개념은 전자석 설계의 매우 중요한 측면입니다.설계가 필요한 것보다 더 많은 듀티 사이클을 제공한다면 최적이 아닙니다.더 많은 듀티 사이클은 본질적으로 더 많은 구리 와이어가 필요하고(결과적으로 더 높은 비용으로) 사용 가능한 클램핑 힘이 더 적음을 의미합니다.
참고: 듀티 사이클이 더 높은 자석은 전력 손실이 적으므로 에너지를 덜 사용하므로 작동 비용이 저렴합니다.그러나 자석이 짧은 시간 동안만 켜져 있기 때문에 작동에 드는 에너지 비용은 일반적으로 거의 중요하지 않은 것으로 간주됩니다.따라서 설계 접근 방식은 코일 권선을 과열하지 않는 측면에서 최대한 많은 전력 손실을 방지하는 것입니다.(이 접근 방식은 대부분의 전자석 설계에 일반적입니다).
Magnabend는 약 25%의 공칭 듀티 사이클을 위해 설계되었습니다.
일반적으로 구부리는 데 2~3초 밖에 걸리지 않습니다.그런 다음 공작물이 재배치되고 다음 굽힘을 위해 준비되는 동안 자석이 8~10초 더 꺼집니다.25% 듀티 사이클을 초과하면 결국 자석이 너무 뜨거워지고 열 과부하가 트립됩니다.자석은 손상되지 않지만 다시 사용하기 전에 약 30분 동안 냉각되어야 합니다.
현장에서 기계에 대한 작동 경험에 따르면 25% 듀티 사이클은 일반 사용자에게 매우 적합합니다.실제로 일부 사용자는 더 적은 듀티 사이클을 희생시키면서 더 많은 클램핑력을 갖는 기계의 선택 사양인 고출력 버전을 요청했습니다.
코일 단면적
코일에 사용할 수 있는 단면적은 장착할 수 있는 구리 와이어의 최대량을 결정합니다. 사용 가능한 영역은 필요한 암페어 회전수 및 전력 손실과 일치하여 필요한 것보다 많아야 합니다.코일에 더 많은 공간을 제공하면 필연적으로 자석의 크기가 증가하고 강철의 자속 경로 길이가 길어집니다(전체 자속이 감소함).
동일한 주장은 설계에 제공된 코일 공간이 무엇이든 항상 구리 와이어로 채워져야 한다는 것을 의미합니다.가득 차 있지 않으면 자석 구조가 더 좋았을 수 있음을 의미합니다.
Magnabend 클램핑 포스:
아래 그래프는 실험적 측정으로 얻은 것이지만 이론적인 계산과 상당히 일치합니다.
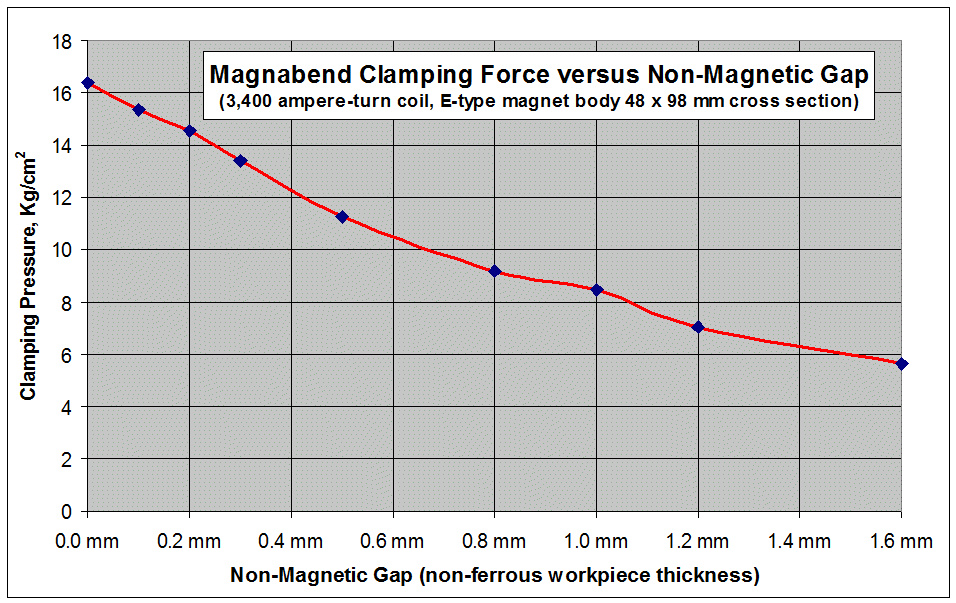
고정력은 다음 공식에서 수학적으로 계산할 수 있습니다.
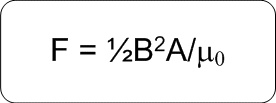
F = 힘(뉴턴)
B = 테슬라의 자속 밀도
A = 극의 면적(m2)
µ0 = 투자율 상수, (4π x 10-7)
예를 들어 2 Tesla의 자속 밀도에 대한 클램핑력을 계산합니다.
따라서 F = ½(2)2 A/µ0
단위 면적(압력)에 대한 힘의 경우 공식에서 "A"를 삭제할 수 있습니다.
따라서 압력 = 2/μ0 = 2/(4π x 10-7) N/m2입니다.
이것은 1,590,000N/m2로 나옵니다.
이것을 킬로그램 힘으로 변환하려면 g(9.81)로 나눌 수 있습니다.
따라서 압력 = 162,080kg/m2 = 16.2kg/cm2입니다.
이것은 위 그래프에 표시된 제로 갭에 대해 측정된 힘과 다소 잘 일치합니다.
이 수치는 기계의 극 면적을 곱하여 주어진 기계에 대한 총 형체력으로 쉽게 변환할 수 있습니다.모델 1250E의 경우 극 영역은 125(1.4+3.0+1.5) = 735 cm2입니다.
따라서 총 제로 갭 힘은 (735 x 16.2) = 11,900kg 또는 11.9톤이 됩니다.자석 길이 미터당 약 9.5톤.
자속 밀도와 클램핑 압력은 직접적인 관련이 있으며 아래 그래프로 표시됩니다.
실제적인 클램핑력:
실제로 이 높은 클램핑력은 필요하지 않을 때(!), 즉 얇은 강철 공작물을 구부릴 때만 실현됩니다.비철금속 소재를 구부릴 때 힘은 위의 그래프와 같이 덜하고 (조금 신기하게도) 두꺼운 강철 소재를 구부릴 때도 더 적습니다.날카로운 굽힘을 만드는 데 필요한 클램핑 힘이 반경 굽힘에 필요한 것보다 훨씬 높기 때문입니다.따라서 굽힘이 진행됨에 따라 클램프 바의 전면 가장자리가 약간 들어 올려져 공작물이 반경을 형성할 수 있습니다.
형성된 작은 에어 갭은 클램핑력의 약간의 손실을 야기하지만 반경 굽힘을 형성하는 데 필요한 힘은 자석 클램핑력보다 더 급격하게 떨어졌습니다.따라서 안정적인 상황이 발생하고 클램프 바가 놓지 않습니다.
위에서 설명한 것은 기계가 두께 한계에 가까울 때 굽힘 모드입니다.더 두꺼운 작업물을 시도하면 물론 클램프 바가 들어 올려집니다.
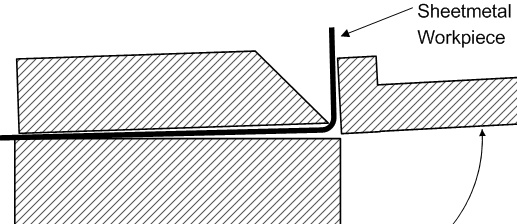
이 다이어그램은 클램프 바의 노즈 에지가 날카롭지 않고 약간 반경이 있는 경우 두꺼운 굽힘을 위한 에어 갭이 감소할 것임을 시사합니다.
실제로 이것이 사실이며 적절하게 만들어진 Magnabend에는 모서리가 둥근 클램프 막대가 있습니다.(반경 모서리는 날카로운 모서리에 비해 우발적인 손상을 입는 경향이 훨씬 적습니다.)
굽힘 실패의 한계 모드:
매우 두꺼운 공작물을 구부리려고 하면 클램프 바가 단순히 들어 올려지기 때문에 기계가 구부리지 못합니다.(다행히 이것은 극적인 방식으로 발생하지 않습니다. 클램프 바가 조용히 갑니다).
그러나 굽힘 하중이 자석의 굽힘 용량보다 약간만 크면 일반적으로 굽힘이 약 60도로 진행되고 클램프 바가 뒤로 미끄러지기 시작합니다.이 고장 모드에서 자석은 공작물과 자석 베드 사이에 마찰을 만들어 간접적으로 굽힘 하중에 저항할 수 있습니다.
리프트오프에 의한 파손과 슬라이딩에 의한 파손의 두께차는 일반적으로 그다지 크지 않다.
리프트 오프 실패는 클램프 바의 앞쪽 가장자리를 위쪽으로 당기는 작업물로 인해 발생합니다.클램프 바의 전면 가장자리에 있는 클램핑력은 주로 이에 저항하는 것입니다.뒤쪽 가장자리의 클램핑은 클램프 바가 회전하는 위치에 가깝기 때문에 거의 효과가 없습니다.실제로 리프트오프에 저항하는 것은 전체 클램핑력의 절반에 불과합니다.
반면에 슬라이딩은 전체 클램핑력에 의해 저항되지만 마찰을 통해서만 이루어지므로 실제 저항은 공작물과 자석 표면 사이의 마찰 계수에 따라 달라집니다.
깨끗하고 건조한 강철의 경우 마찰 계수는 0.8만큼 높을 수 있지만 윤활이 있는 경우 0.2만큼 낮을 수 있습니다.일반적으로 굽힘 파손의 한계 모드는 일반적으로 슬라이딩으로 인한 것이지만 자석 표면의 마찰을 증가시키려는 시도는 가치가 없는 것으로 밝혀졌습니다.
두께 용량:
폭 98mm, 깊이 48mm 및 3,800암페어 회전 코일이 있는 E형 자석 본체의 경우 전체 길이 굽힘 용량은 1.6mm입니다.이 두께는 강판과 알루미늄 판 모두에 적용됩니다.알루미늄 시트에 대한 클램핑은 덜하지만 구부리는 데 더 적은 토크가 필요하므로 두 유형의 금속에 대해 유사한 게이지 용량을 제공하는 방식으로 보상합니다.
명시된 굽힘 용량에 대한 몇 가지 주의 사항이 필요합니다. 주요 사항은 판금의 항복 강도가 크게 다를 수 있다는 것입니다.1.6mm 용량은 최대 250MPa의 항복 응력을 갖는 강철과 최대 140MPa의 항복 응력을 갖는 알루미늄에 적용됩니다.
스테인레스 스틸의 두께 용량은 약 1.0mm입니다.스테인리스 스틸은 일반적으로 비자성이지만 상당히 높은 항복 응력을 갖기 때문에 이 용량은 대부분의 다른 금속보다 훨씬 적습니다.
또 다른 요인은 자석의 온도입니다.자석이 뜨거워지면 코일의 저항이 더 높아져 전류가 덜 흐르게 되어 결과적으로 더 낮은 암페어 회전수와 더 낮은 조임력이 발생합니다.(이 효과는 일반적으로 매우 보통이며 기계가 사양을 충족하지 못하게 할 가능성은 거의 없습니다.)
마지막으로 자석 단면을 더 크게 만들면 더 두꺼운 용량의 Magnabends를 만들 수 있습니다.
